Levi Haupert

NLOPredict

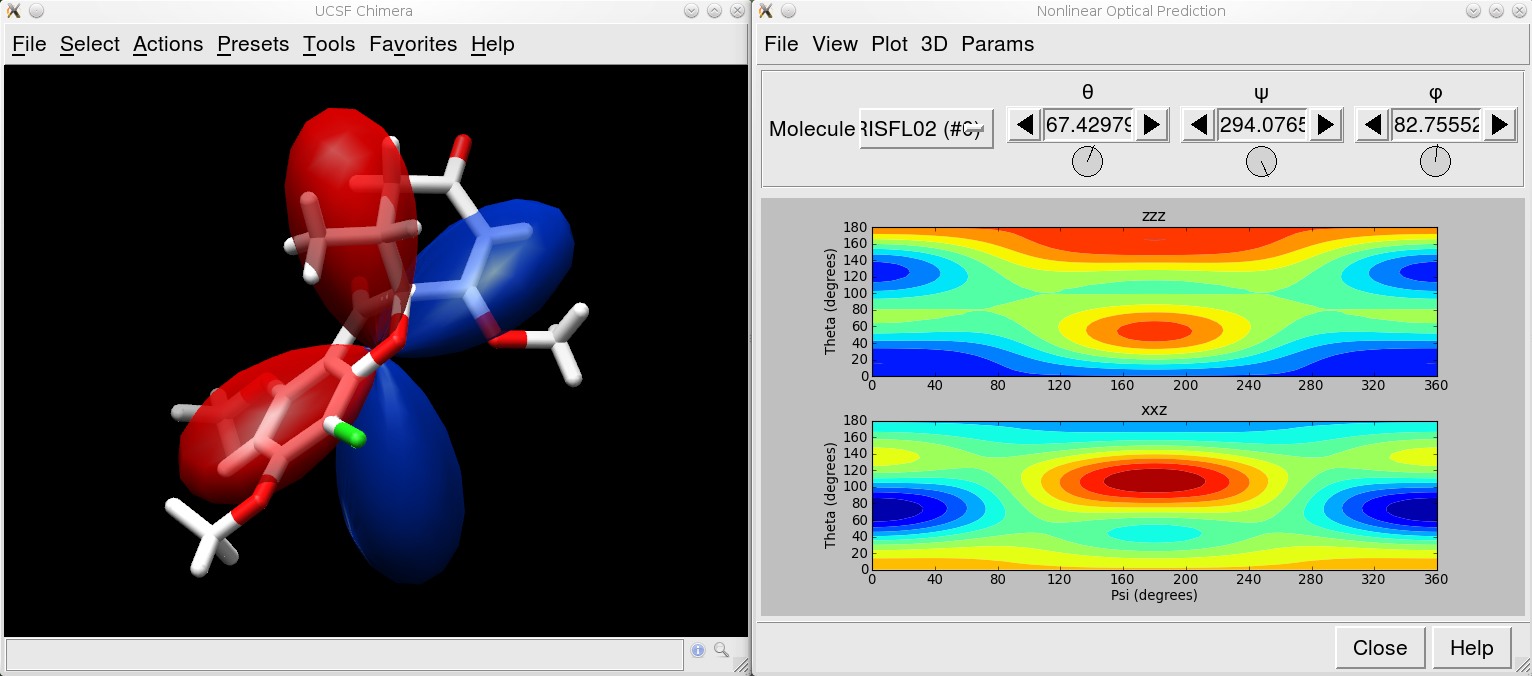
I'm the primary administrator for NLOPredict, a scientific program for calculation and visualization of nonlinear optical properties of molecules and crystals. Most of the information pertaining to NLOPredict lives elswhere and I'm not going to reproduce it here.

Project Page
Web Page
Blog

Karlsson

I configured a computer cluster for computational chemistry for the Slipchenko group. I'll add more details about Karlsson later, including a tutorial on cluster building. Lyudmila named it Karlsson after Karlsson-on-the-Roof.

Semi-helpful document for Karlsson specific things.

I don't have a cluster-building tutorial ready, yet. Frankly, I'm not sure if I can add a whole lot to the information that's already out there. Until I figure out my unique contribution, I'll just provide some resources that I found useful while constructing Karlsson.

Linux-based cluster guide
Oregon State University sample cluster
Cluster Resources (caretakers of TORQUE and MAUI)
Debian-based TORQUE turorial
Indepth description of computer networking
Quick HOWTO for DHCP servers
HOWTO for NFS
Detailed reference for NIS

Tools

I'll post some useful scripts and code for doing scientific things here when I get a chance. I wrote one a while back to find a rotation matrix connecting two vectors. I write scripts all the time, but this is one I think it might be generally useful. I appreciate any feedback. Let me know if I just reinvented the wheel.

			
# LMH 2/2/2010

# Import the math functions we'll need from numpy
from numpy import array, dot, cross, zeros
from numpy import sin, cos, arccos, sqrt

def rotVec(vec1, vec2):
	"""A function to create a rotation 
	   matrix for rotating a 3D vector,
	   (vec1) into another (vec2)returns
	   a 3x3 numpy rotation matrix"""  
	
	# find magnitudes of input vectors

	vec1mag = sqrt(dot(vec1, vec1))
	vec2mag = sqrt(dot(vec2, vec2))
	
    # find the angle between vec1 and vec2

	angle = arccos(dot(vec1, vec2) /
	               (vec1mag * vec2mag))
	
    # find perpendicular axis using cross product

	axis = cross(vec2, vec1)
	
    # normalize axis vector to make unit 
    # vector for rotation matrix

	u = (axis / sqrt(dot(axis, axis)))  

	c = cos(angle)
	s = sin(angle)

	R = zeros([3,3], float)

	R[0, 0] = u[0] ** 2 + (1 - u[0] ** 2) * c    
	R[0, 1] = u[0] * u[1] * (1 - c) - u[2] * s
	R[0, 2] = u[0] * u[2] * (1 - c) + u[1] * s
	R[1, 0] = u[0] * u[1] * (1 - c) + u[2] * s
	R[1, 1] = u[1] ** 2 + (1 - u[1] ** 2) * c    
	R[1, 2] = u[1] * u[2] * (1 - c) - u[0] * s
	R[2, 0] = u[0] * u[2] * (1 - c) - u[1] * s
	R[2, 1] = u[1] * u[2] * (1 - c) + u[0] * s
	R[2, 2] = u[2] ** 2 + (1 - u[2] ** 2) * c  
	
	return R
				

Code prettified by google-code-prettify.